30 December 2017
23 December 2017
16 December 2017
Hacking Jupyter Notebook HTML for Blogger
One thing Blogger sucks at is formatting code and mathematics. This is something Jupyter notebooks excel at. What I want is a way to turn a Jupyter notebook into a blog post in Blogger so I can poke around with math and programming, document it, and then post my findings where no one actually reads them (but they could!). Fortunately, Blogger does offer a way to edit HTML directly, which means it is possible to modify an HTML export from a Jupyter notebook, then cut and paste that into the HTML editor in Blogger. Or, in a fact-finding mission, paste the entirety of the HTML export into blogger, see what happens, then edit and iterate.
This is what I did for my post on iterative v. closed form Fibonacci calculations. I learned a lot hacking CSS for that post, but one thing I failed to do is try to embed the Jupyter notebook HTML within text written in blogger. Say this post.
Here's what happens when you try to embed Jupyter notebook generated HTML inside a Blogger post with text already in it:
Looking at the HTML source directly, there are some obvious things we can remove:
Didn't really help. Our blog format right margin is being ignored. Since it's a formatting issue, searching the inline CSS for 'width' seemed like a prudent thing to do.
There are a lot of 'width' values in the CSS. Most are percentages of something, so can be safely ignored. The ones that grabbed my attention were min-width values in pixels in at-statements, such as "@media (min-width: 768px) {...}". If you remove everything within the parentheses on statements like this, the formatting becomes:
Now we're getting somewhere. The Jupyter notebook HTML separates itself from the blog post proper, but that might not be a bad thing. However, if I want to get rid of it, the outermost <div> tag is the most likely candidate for removal. That would be <div tabindex="-1" id="notebook" class="border-box-sizing"> and, presumably, the last </div> in the HTML...
...Only, that doesn't work. I forwent the screen capture because it looks like the previous one, and I got to use the word "forwent" in a sentence. Twice.
Pruning that much HTML should make the notebook embed-able between "standard" blogger markup, too:
At any rate, knowing this is good enough to start automating the pruning of Jupyter notebook-generated HTML. Then I can play in Jupyter notebook, save the notebook to HTML, push the HTML through my script, then copy and paste it into a Blogger post.
I believe the British call this a bodge. The act of creating a bodge is bodging. And the code for this bodge can be found on GitHub, here.
A bodge, according to Merriam-Webster, is also "about half a peck".
A peck is a quarter bushel.
And a bushel, according to Merriam-Webster, is "any of various units of dry capacity".
Is it no wonder most of the world switched to SI units?
This is what I did for my post on iterative v. closed form Fibonacci calculations. I learned a lot hacking CSS for that post, but one thing I failed to do is try to embed the Jupyter notebook HTML within text written in blogger. Say this post.
Here's what happens when you try to embed Jupyter notebook generated HTML inside a Blogger post with text already in it:
 |
| That ain't right. |
- <!DOCTYPE html>
- <html> and </html>
- <head> and </head>, though we probably want to keep the <script> tags inside <head>. The <title> tag and everything in between it and its closing tag can go, though. <meta> can probably go, too.
 |
| Obvious edits. |
Didn't really help. Our blog format right margin is being ignored. Since it's a formatting issue, searching the inline CSS for 'width' seemed like a prudent thing to do.
There are a lot of 'width' values in the CSS. Most are percentages of something, so can be safely ignored. The ones that grabbed my attention were min-width values in pixels in at-statements, such as "@media (min-width: 768px) {...}". If you remove everything within the parentheses on statements like this, the formatting becomes:
 |
| Eureka! |
Now we're getting somewhere. The Jupyter notebook HTML separates itself from the blog post proper, but that might not be a bad thing. However, if I want to get rid of it, the outermost <div> tag is the most likely candidate for removal. That would be <div tabindex="-1" id="notebook" class="border-box-sizing"> and, presumably, the last </div> in the HTML...
...Only, that doesn't work. I forwent the screen capture because it looks like the previous one, and I got to use the word "forwent" in a sentence. Twice.
Pruning that much HTML should make the notebook embed-able between "standard" blogger markup, too:
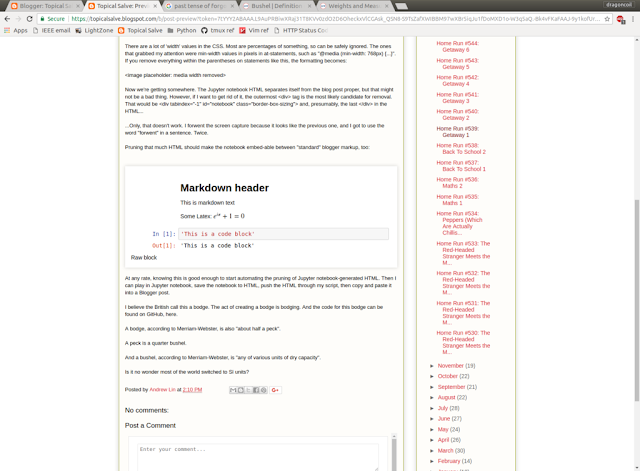 |
| Looks well behaved. |
At any rate, knowing this is good enough to start automating the pruning of Jupyter notebook-generated HTML. Then I can play in Jupyter notebook, save the notebook to HTML, push the HTML through my script, then copy and paste it into a Blogger post.
I believe the British call this a bodge. The act of creating a bodge is bodging. And the code for this bodge can be found on GitHub, here.
A bodge, according to Merriam-Webster, is also "about half a peck".
A peck is a quarter bushel.
And a bushel, according to Merriam-Webster, is "any of various units of dry capacity".
Is it no wonder most of the world switched to SI units?
Labels:
programming
Iterative v Closed Form Fibonacci Calculations
The Fibonnaci sequence is a wonderous thing. I have used it as the basis of an interview question, and have seen more surprising implementations than I thought possible. I even quipped to one candidate that if someone implemented the closed form solution, I would stop the interview and recommend hire right then and there. To date, though, no one has ever offered a closed form solution.
There's good reason for this (besides no one knowing the closed form solution off the top of their head). For computational purposes, the closed form solution for the nth Fibonacci number is
$$F(n) = \left[\frac{\phi^n}{\sqrt{5}}\right]$$
Where $\phi$ is the Golden Ratio,
$$\phi = \frac{1 + \sqrt{5}}{2}$$
and $[ ]$ represents the rounding operation.
Both $\phi$ and $\sqrt{5}$ are irrational, so rounding error is going to bite you.
But how soon does this happen? It's simple enough to find out programatically.
There's good reason for this (besides no one knowing the closed form solution off the top of their head). For computational purposes, the closed form solution for the nth Fibonacci number is
$$F(n) = \left[\frac{\phi^n}{\sqrt{5}}\right]$$
Where $\phi$ is the Golden Ratio,
$$\phi = \frac{1 + \sqrt{5}}{2}$$
and $[ ]$ represents the rounding operation.
Both $\phi$ and $\sqrt{5}$ are irrational, so rounding error is going to bite you.
But how soon does this happen? It's simple enough to find out programatically.
In [1]:
# Assuming Python 3.6+!
import math
def fib_iter(n: int) -> int:
"""Return the nth Fibonacci number. Calculated iteratively."""
f0 = f1 = 1
for x in range(1, n):
f0, f1 = f1, f0 + f1
return f0
def fib_closed(n: int) -> int:
"""Return the nth Fibonacci number. Closed form."""
sqrt_5 = math.sqrt(5)
phi = (1 + sqrt_5) / 2
f = math.floor((phi ** n / sqrt_5) + 0.5)
return f
In [2]:
def test_equivalent(max_n: int, fib_a, fib_b):
"""Compare Fibonnaci calulators up to max_n."""
for n in range(1, max_n):
if fib_a(n) != fib_b(n):
return f'not equivalent at n={n}.'
return 'equivalent in test range.'
In [3]:
test_equivalent(1000, fib_iter, fib_closed)
Out[3]:
'not equivalent at n=71.'
So on my computer, the closed form breaks down at the 71st Fibonacci number. Not so great.
In Python, floats are usually represented as IEEE-754 double precision values. Numpy doesn't offer better than 64-bit floats -- that is, IEEE-754 double precision values -- so it won't be of any help to us. That leads us to the decimal library (https://docs.python.org/3/library/decimal.html).
We can rewrite fib_closed thus:
In Python, floats are usually represented as IEEE-754 double precision values. Numpy doesn't offer better than 64-bit floats -- that is, IEEE-754 double precision values -- so it won't be of any help to us. That leads us to the decimal library (https://docs.python.org/3/library/decimal.html).
We can rewrite fib_closed thus:
In [4]:
import decimal
def fib_closed_decimal(n: int) -> int:
sqrt_5 = decimal.Decimal(5).sqrt()
phi = (decimal.Decimal(1) + sqrt_5) / decimal.Decimal(2)
f = phi ** decimal.Decimal(n) / sqrt_5
f = int(f.to_integral_value(rounding=decimal.ROUND_HALF_UP))
return f
In [5]:
test_equivalent(1000, fib_iter, fib_closed_decimal)
Out[5]:
'not equivalent at n=123.'
We now break at the 123rd Fibonacci number.
But that's just with the default precision. The decimal library has the concept of context, where you can set your precision. Up to the point you can get memory errors on calculations, in fact.
So how many decimal places of precision do we need to compute the first 1000 Fibonacci numbers correctly in the closed form?
But that's just with the default precision. The decimal library has the concept of context, where you can set your precision. Up to the point you can get memory errors on calculations, in fact.
So how many decimal places of precision do we need to compute the first 1000 Fibonacci numbers correctly in the closed form?
In [6]:
with decimal.localcontext() as ctx:
# 28 is the default precision according to docs, but there
# isn't a defined constant for it.
for p in range(28, decimal.MAX_PREC):
ctx.prec = p
result = test_equivalent(1000, fib_iter, fib_closed_decimal)
if result.startswith('equivalent'):
print(f'required precision={p}')
break
required precision=212
We need (on my computer) 212 decimal places of precison.
This is good. We can reliably compute the nth Fibonacci number in O(1) instead of O(n) for n < 1000, which is good enough for interview questions. But how efficient is it, really? The decimal library must be pretty heavy, so where is the break even point?
Again, it's easy to test this directly, but first we should optimize the implementation of the closed form solution. There's no sense calculating the values for $\sqrt{5}$ and $\phi$ over and over again since they're effectively constants. Heck, that's two-thirds of the calculations right there! To do that, a class is in order.
This is good. We can reliably compute the nth Fibonacci number in O(1) instead of O(n) for n < 1000, which is good enough for interview questions. But how efficient is it, really? The decimal library must be pretty heavy, so where is the break even point?
Again, it's easy to test this directly, but first we should optimize the implementation of the closed form solution. There's no sense calculating the values for $\sqrt{5}$ and $\phi$ over and over again since they're effectively constants. Heck, that's two-thirds of the calculations right there! To do that, a class is in order.
In [7]:
class Fibonacci:
def __init__(self):
self.sqrt_5 = decimal.Decimal(5).sqrt()
self.phi = (decimal.Decimal(1) + self.sqrt_5) / decimal.Decimal(2)
def fib(self, n: int) -> int:
"""Return the nth Fibonacci number."""
f = self.phi ** decimal.Decimal(n) / self.sqrt_5
f = int(f.to_integral_value(rounding=decimal.ROUND_HALF_UP))
return f
Before we run, let's make sure our code is equivalent.
In [8]:
with decimal.localcontext() as ctx:
ctx.prec = 212
f = Fibonacci()
print(test_equivalent(1000, fib_closed_decimal, f.fib))
equivalent in test range.
In [9]:
%matplotlib inline
In [10]:
import timeit
import matplotlib.pyplot as plt
In [11]:
num = 250
x = list(range(1, 500))
iter_times = [
timeit.timeit(f'fib_iter({n})', number=num, globals=globals())
for n in x
]
with decimal.localcontext() as ctx:
ctx.prec = 212
f = Fibonacci()
closed_times = [
timeit.timeit(f'f.fib({n})', number=num, globals=globals())
for n in x
]
In [12]:
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x, iter_times, 'r', x, closed_times, 'b')
ax.set_xlabel('n')
ax.set_ylabel('Execution time (seconds)')
ax.legend(['iterative', 'closed form'])
ax.set_title(f'Time for {num} calculations of Fib(n)')
Out[12]:
<matplotlib.text.Text at 0x7f08b0070b38>
The break even point (again, on my computer) is in the range [320, 360], and the closed form looks to be more O(log(n)) than O(1). Like I said, the decimal library is pretty heavy.
So is the closed form solution worth it? In the context of an interview question, absolutely. It opens discussion of rounding errors, execution time, and memory requirements. And I bet an interviewer who asks you to code up Fibonacci has never been given the closed form solution.
So is the closed form solution worth it? In the context of an interview question, absolutely. It opens discussion of rounding errors, execution time, and memory requirements. And I bet an interviewer who asks you to code up Fibonacci has never been given the closed form solution.
Labels:
math,
mathematics,
maths,
programming
Subscribe to:
Posts (Atom)








